前言

之所以说这是梦想开始的地方，是因为这是我一个月前在 LeetCode 上刷的第一道算法题。

这是 LeetCode 上 2 月 19 日的每日一题，当时对算法的技巧一窍不通的我点开了他，思考了五分钟，发现似乎无法用暴力方法解决它。

当我点开解答时，惊呆了，怎么会有这么巧妙的方法，而且还给出了同类题目的解体模板，我简直是小刀划屁屁——开了眼了。

由于前几天一直忙于教研室的工作和博客网页的优化，所以没有刷题，现在忙得也差不多了，可以重新开始 LeetCode 之旅了，就想再感受一次当初的那份惊艳。

原题

给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。

返回仅包含 1 的最长（连续）子数组的长度。

示例 1：

1
2
3
4
5
输入：A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出：6
解释：
[1,1,1,0,0,1,1,1,1,1,1]
下标为 5,10 的数字从 0 翻转到 1，最长的子数组长度为 6。

示例 2：

1
2
3
4
5
输入：A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出：10
解释：
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
下标为 4, 5, 9 的数字从 0 翻转到 1，最长的子数组长度为 10。

解题思路

题意转换。把「最多可以把 K 个 0 变成 1，求仅包含 1 的最长子数组的长度」转换为 「找出一个最长的子数组，该子数组内最多允许有 K 个 0 」。

这一步的题意转换让我想起了高中数学老师讲圆锥曲线题目的解法，难题往往难在对题目描述的转化上，只要把未知问题转化为已知问题，难题也就迎刃而解了。

经过上面的题意转换，我们可知本题是求最大连续子区间，可以使用滑动窗口方法。滑动窗口的限制条件是：窗口内最多有 K 个 0。

代码思路：

  • 使用 left 和 right 两个指针，分别指向滑动窗口的左右边界。
  • right 主动右移：right 指针每次移动一步。当 A[right] 为 0，说明滑动窗口内增加了一个 0；
  • left 被动右移：判断此时窗口内 0 的个数，如果超过了 K，则 left 指针被迫右移，直至窗口内的 0 的个数小于等于 K 为止。
  • 滑动窗口长度的最大值就是所求。

示例

以 A= [1,1,1,0,0,0,1,1,1,1,0], K = 2 为例，下面的动图演示了滑动窗口的两个指针的移动情况。
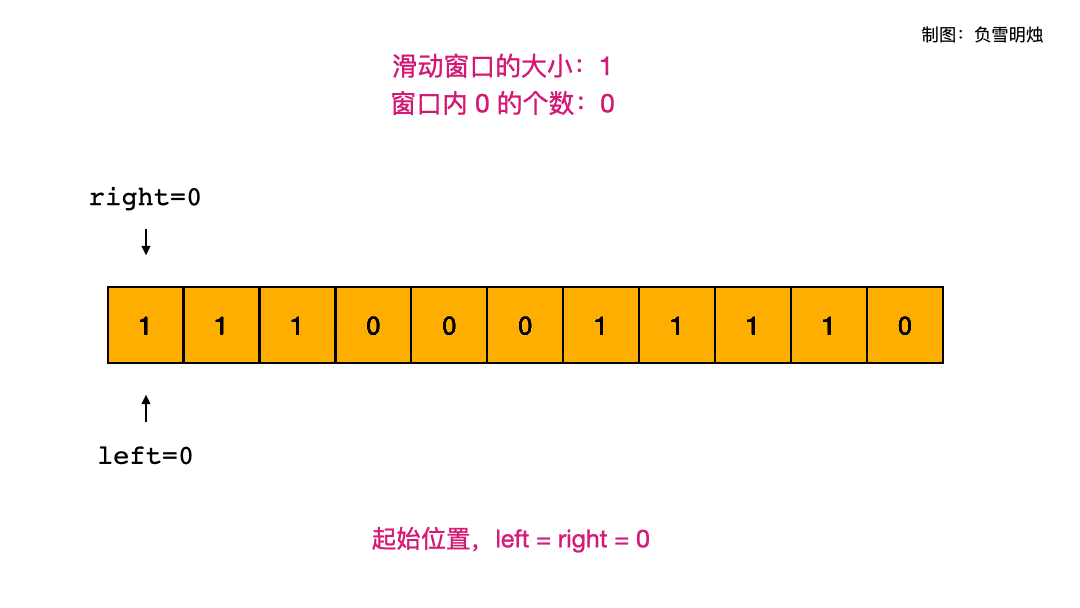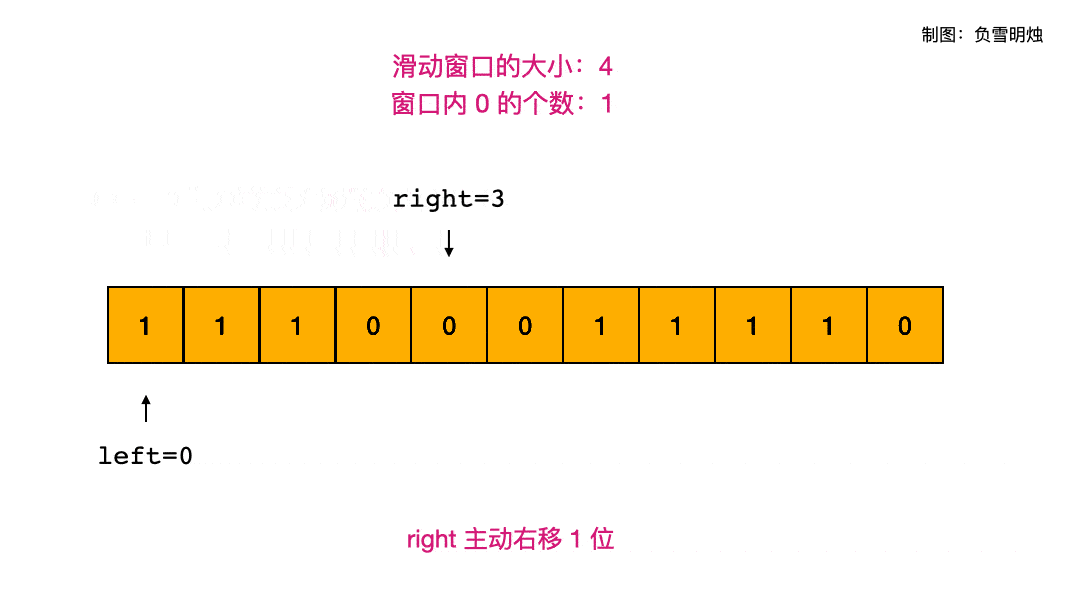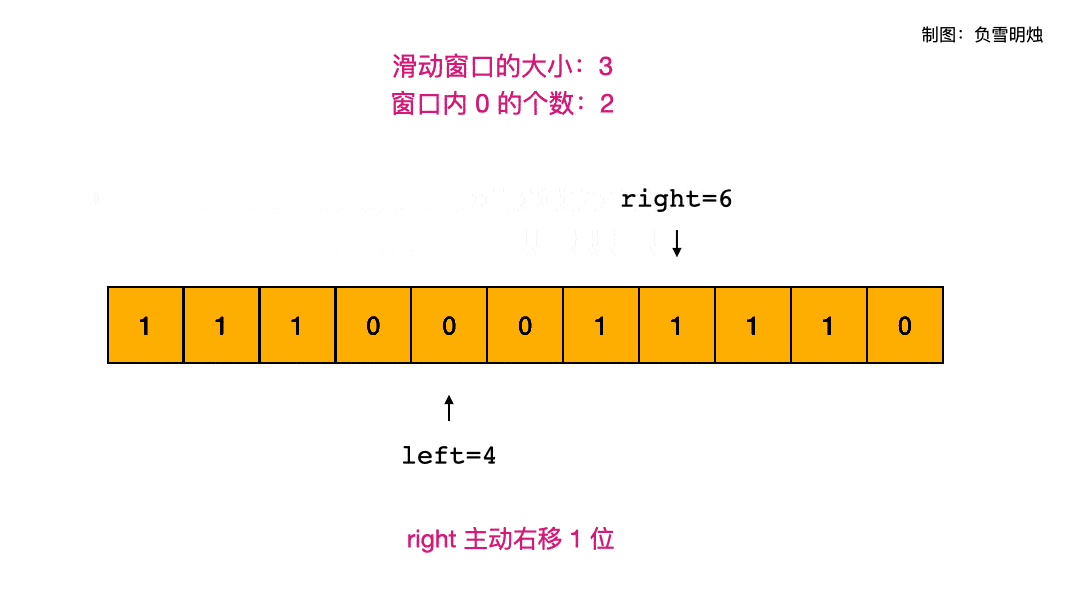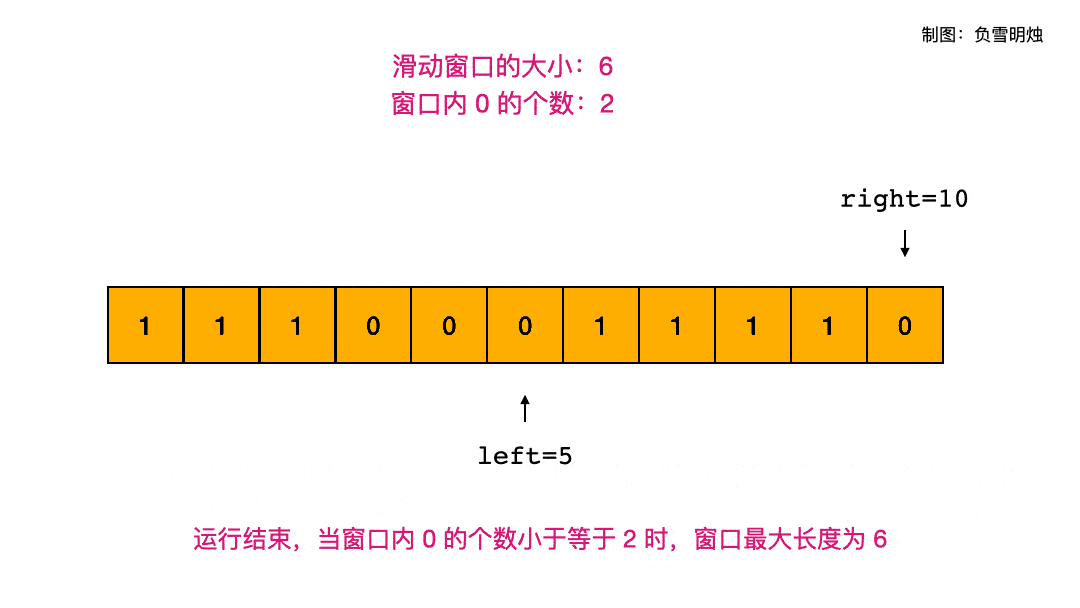
sliding-window

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int longestOnes(int[] A, int K) {
        int N = A.length;
        int res = 0;
        int left = 0, right = 0;
        int zeros = 0;
        while (right < N) {
            if (A[right] == 0)
                zeros ++;
            while (zeros > K) {
                if (A[left++] == 0)
                    zeros --;
            }
            res = Math.max(res, right - left + 1);
            right ++;
        }
        return res;
    }
}

滑动窗口模板

《挑战程序设计竞赛》这本书中把滑动窗口叫做「虫取法」，我觉得非常生动形象。因为滑动窗口的两个指针移动的过程和虫子爬动的过程非常像：前脚不动，把后脚移动过来；后脚不动，把前脚向前移动。

我分享一个滑动窗口的模板，能解决大多数的滑动窗口问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int slidingWindow(int[] nums) {
    int N = nums.length; // 数组/字符串长度
    int left, right = 0, 0; // 双指针，表示当前遍历的区间[left, right]，闭区间
    int sums = 0; // 用于统计 子数组/子区间 是否有效，根据题目可能会改成求和/计数
    int res = 0; // 保存最大的满足题目要求的 子数组/子串 长度
    while (right < N) { // 当右边的指针没有搜索到 数组/字符串 的结尾
        sums += nums[right]; // 增加当前右边指针的数字/字符的求和/计数
        while (区间[left, right]不符合题意) { // 此时需要一直移动左指针，直至找到一个符合题意的区间
            sums -= nums[left]; // 移动左指针前需要从counter中减少left位置字符的求和/计数
            left += 1; // 真正的移动左指针，注意不能跟上面一行代码写反
        } // 到 while 结束时，我们找到了一个符合题意要求的 子数组/子串
        res = Math.max(res, right - left + 1); // 需要更新结果
        right += 1; // 移动右指针，去探索新的区间
    }
    return res;
}

滑动窗口中用到了左右两个指针，它们移动的思路是：以右指针作为驱动，拖着左指针向前走。右指针每次只移动一步，而左指针在内部 while 循环中每次可能移动多步。右指针是主动前移，探索未知的新区域；左指针是被迫移动，负责寻找满足题意的区间。

模板的整体思想是：

  1. 定义两个指针 left 和 right 分别指向区间的开头和结尾，注意是闭区间；定义 sums 用来统计该区间内的各个字符出现次数；
  2. 第一重 while 循环是为了判断 right 指针的位置是否超出了数组边界；当 right 每次到了新位置，需要增加 right 指针的求和/计数；
  3. 第二重 while 循环是让 left 指针向右移动到 [left, right] 区间符合题意的位置；当 left 每次移动到了新位置，需要减少 left 指针的求和/计数；
  4. 在第二重 while 循环之后，成功找到了一个符合题意的 [left, right] 区间，题目要求最大的区间长度，因此更新 res 为 max(res, 当前区间的长度) 。
  5. right 指针每次向右移动一步，开始探索新的区间。

模板中的 sums 需要根据题目意思具体去修改，本题是求和题目因此把 sums 定义成整数用于求和；如果是计数题目，就需要改成字典用于计数。当左右指针发生变化的时候，都需要更新 sums 。

另外一个需要根据题目去修改的是内层 while 循环的判断条件，即： 区间 [left, right][left,right] 不符合题意 。对于本题而言，就是该区间内的 0 的个数超过了 2 。